Assignment 5¶

Sayan Mondal¶

Number of late days used : 2¶

two.png

Q1. Classification Model (40 points)¶

  • Report the test accuracy of your best model.

Test accuracy of my best classification model: 97.796%

  • Visualize a few random test point clouds and mention the predicted classes for each. Also, visualize at least 1 failure prediction for each class (chair, vase and lamp), and provide interpretation in a few sentences.

Successful predictions of chair:

Successful predictions of vase:

Successful predictions of lamp:

Failed prediction examples:

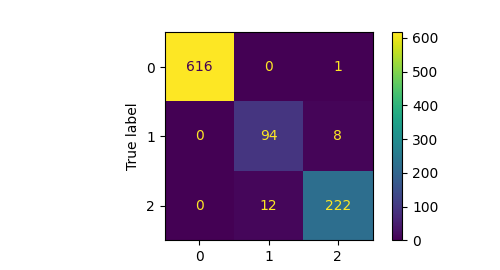
Confusion Matrix: confusion-matrix

Interpretation:

The classification for these three classes, namely chair (label 0), vase (label 1) and lamp (label 2), yielded pretty good results.

From the confusion matrix it is evident tha the classification model sometimes make wrong predictions between vases and lamps. On the other hand the model predicts chair almost perfectly.

This could be due to the fact that lamps and vases have somewhat similar geometry, and it is sometimes hard to differentiate even for humans without any texture information. Chairs, on the other hand, have very different structure as compared to vases and lamps.

Another reason is the unbalanced testing/training dataset. The chair class is much larger than the other two classes. There are 4489 chairs, 741 vases and 1554 lamps in the test data and the learned model is tested on 617 chairs, 102 vases, and 234 lamps. This data unbalance also affects our results.

Q2. Segmentation Model (40 points)¶

  • Report the test accuracy of your best model.

Test accuracy of my best segmentation model: 90.171%

  • Visualize segmentation results of at least 5 objects (including 2 bad predictions) with corresponding ground truth, report the prediction accuracy for each object, and provide interpretation in a few sentences.

Top 5 successful predictions with corresponding ground truth:

Test accuracy of object: 99.67%

pred gt

Test accuracy of object: 99.62%

pred gt

Test accuracy of object: 99.35%

pred gt

Test accuracy of object: 99.33%

pred gt

Test accuracy of object: 99.33%

pred gt

Top 5 bad predictions with corresponding ground truth:

Test accuracy of object: 43.04%

pred gt

Test accuracy of object: 48.54%

pred gt

Test accuracy of object: 51.39%

pred gt

Test accuracy of object: 51.41%

pred gt

Test accuracy of object: 52.73%

pred gt

Interpretation:

Since we are sampling 10000 points randomly, which is not a lot, and the segmetation model is making the part segmentation predictions based on them, some of the chairs which need more points to have a denser reprentation are being poorly segmented as we can see from the above examples.

Q3. Robustness Analysis (20 points)¶

Testing of model robustness with varying the number of points per object¶

  • Procedure: To test with different number of sampled points by modifying --num_points during evaluation.
  • Results:
  • Test accuracy
Number of points Classification test accuracy Segmentation test accuracy
10000 97.796% 90.171%
1000 97.377% 89.892%
100 93.494% 83.240%
10 28.226% 67.812%
1 24.554% 55.105%

Clearly, with less number of points per object the test accuracy drops, both in classification and in segmentation task.

  • Visualization on a few samples:
10000 pts 1000 pts 100 pts 10 pts 1 pt
10000 pts 1000 pts 100 pts 10 pts 1 pt
10000 pts 1000 pts 100 pts 10 pts 1 pt
  • Interpretation: The classification model learns from an unbalanced dataset(4489 chairs, 741 vases , 1554 lamps). There is a therefore a bias in the learned model. For a fewer number of points (10 pts, 1pt), the model always predicts the object to be a lamp.
gt:10000 pts gt:1000 pts gt:100 pts gt:10 pts gt:1 pt
99.35% part seg accuracy pred:10000 pts 99.20% part seg accuracy pred:1000 pts 97.00% part seg accuracy pred:100 pts 100.00% part seg accuracy pred:10 pts 100.00% part seg accuracy pred:1 pt
  • Interpretation: As stated in PointNet paper, the model has robustness to sampling. This is becasue the global features are still extractable with the reduced sampled points.

Testing of model robustness to various rotations about Z-axis¶

  • Procedure: adding various rotations about Z-axis on the test data.

Code:
relative_rotation = pytorch3d.transforms.euler_angles_to_matrix(torch.tensor([0, 0, rotz_rad]), "XYZ")
test_data[:,]= test_data[:,] @ relative_rotation

  • Results:
  • Test accuracy
Rotation about Z (degrees) Classification test accuracy Segmentation test accuracy
0 97.796% 90.171%
30 62.434% 71.794%
60 32.109% 55.076%
90 20.76% 38.233%

Clearly, with more degrees of rotation, the test accuracy falls, both in classification and in segmentation task.

  • Visualization for classification - example 1:
$\theta_Z$ = 0 $\theta_Z$ = 30 $\theta_Z$ = 60 $\theta_Z$ = 90
  • Visualization for classification - example 2:
$\theta_Z$ = 0 $\theta_Z$ = 30 $\theta_Z$ = 60 $\theta_Z$ = 90
  • Visualization for classification - example 3:
$\theta_Z$ = 0 $\theta_Z$ = 30 $\theta_Z$ = 60 $\theta_Z$ = 90
  • Interpretation: The classification model learns a bias. Due to data imbalance and less stuctural pattern in vases, the model predicts everything which lies in the out-of-data-distribution to be vases. This can be seen in the above examples when the objects are rotated which the model has never seen during its training.

Visualisation for segmentation:

gt: $\theta_Z$ = 0 gt: $\theta_Z$ = 30 gt: $\theta_Z$ = 60 gt: $\theta_Z$ = 90
pred: $\theta_Z$ = 0
99.35% part seg accuracy 		pred: $\theta_Z$ = 30
83.95% part seg accuracy 		pred: $\theta_Z$ = 60
63.15% part seg accuracy 		pred: $\theta_Z$ = 90
44.64% part seg accuracy
  • Interpretation: The segmentation model is quite fragile to rotations as can be seen from the above example.

Testing of model robustness to Gaussian noise¶

  • Procedure: adding gaussian noise with zero mean and different standard deviation to the test dataset.

Code:
torch.normal(mean=0, std = sigma * torch.ones_like(test_data))

  • Results:
  • Test accuracy
$\sigma$ (standard deviation of zero-mean Gaussian Noise) Classification test accuracy Segmentation test accuracy
0.00 97.796% 90.171%
0.01 97.271% 89.917%
0.05 89.612% 83.147%
0.10 83.631% 64.766%
0.50 64.743% 46.299%
1.00 64.743% 42.223%
5.00 64.743% 37.083%
100.00 64.743% 35.670%

Clearly, as expecetded with higher standared deviation, the test accuracy drops, both in classification and in segmentation task. Suprisingly, the test accuracy stops reducing on further adding noise beyond a certain point (stays at 64.743%).

Visualisation for classification - example 1:

$\sigma$ = 0.00 $\sigma$ = 0.01 $\sigma$ = 0.05 $\sigma$ = 0.10
$\sigma$ = 0.50 $\sigma$ = 1.00 $\sigma$ = 5.00 $\sigma$ = 100.00

Visualisation for classification - example 2:

$\sigma$ = 0.00 $\sigma$ = 0.01 $\sigma$ = 0.05 $\sigma$ = 0.10
$\sigma$ = 0.50 $\sigma$ = 1.00 $\sigma$ = 5.00 $\sigma$ = 100.00

Visualisation for classification - example 3:

$\sigma$ = 0.00 $\sigma$ = 0.01 $\sigma$ = 0.05 $\sigma$ = 0.10
$\sigma$ = 0.50 $\sigma$ = 1.00 $\sigma$ = 5.00 $\sigma$ = 100.00
  • Interpretation: The classification model is quite robust to noise. Upto $\sigma = 0.10$, when the structure of the object in the point cloud is still retained the model mostly predicts accurately. For larger noise $\sigma >= 0.50$, there is no stucture/ geometry of the object (its just a ball of points). In such cases, the model has learned a bias that predicts the ball of points to be chairs!

Visualisation for segmentation:

gt: $\sigma$ = 0.00 gt: $\sigma$ = 0.01 gt: $\sigma$ = 0.05 gt: $\sigma$ = 0.10
pred: $\sigma$ = 0.00
99.35% part seg accuracy 		pred: $\sigma$ = 0.01
99.12% part seg accuracy 		pred: $\sigma$ = 0.05
91.92% part seg accuracy 		pred: $\sigma$ = 0.10
82.09% part seg accuracy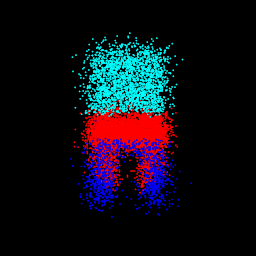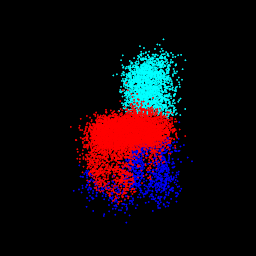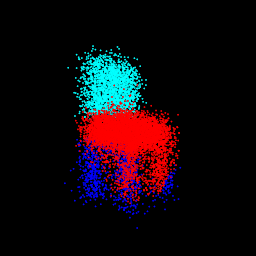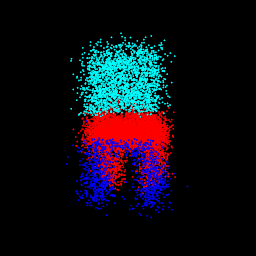
gt: $\sigma$ = 0.50 gt: $\sigma$ = 1.00 gt: $\sigma$ = 5.00 gt: $\sigma$ = 100.00
pred: $\sigma$ = 0.50
56.03% part seg accuracy 		pred: $\sigma$ = 1.00
48.74% part seg accuracy 		pred: $\sigma$ = 5.00
43.96% part seg accuracy 		pred: $\sigma$ = 100.00
42.27% part seg accuracy
  • Interpretation: PointNet still preserves certain classification and segmentation capabilities with heavy noise contamination upto a certain point ($\sigma = 0.1$). We can thus conclude that PointNet is robust to Gaussian noises.

Q4. Expressive architectures (10 points + 20 bonus points)¶

Point Net ++

Implemented PointNet++ architecture for classification to incorporate locality in the vanilla PointNet architecture.

The PointNet++ architecture has the following components:

  • Set Abstraction layer: The PointNet++ architecture is built using a Farthest Sampling technique to sample points from the previous layers or the actual point cloud. The radius of the ball is set to 0.4 and 3. Set abstraction layers are used with MLPs [64, 64, 128] , [128, 128, 256] and [256, 512, 1024] respectively.
  • Vanilla PointNet: Find points of the point cloud which are closest and within a certain threshold to these centroids. After taking these grouped points, find features using a small MLP PointNet. We repeat the above steps multiple times and then eventually use a simple MLP network with batch-normalisation and dropout layers to get a class probability. The output is of shape Bx1xnum_classes. Here, num_classes=3.

The network is then trained using CrossEntropyLoss.

Test accuracy of my best classification model for PointNet was: 97.796%
Test accuracy of my best classification model for PointNet++ is: 98.306%

Visualisation:

PointNet PointNet ++
PointNet PointNet ++

Interpretation:

We observe that Pointnet++ performs slighly better than Pointnet.