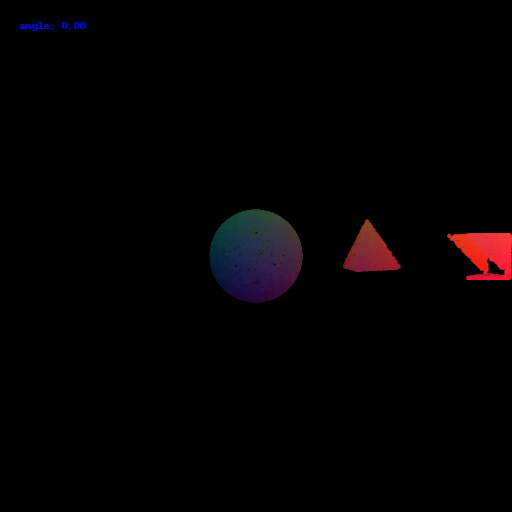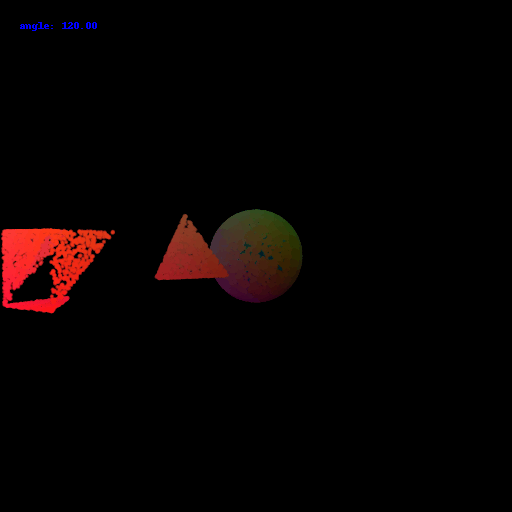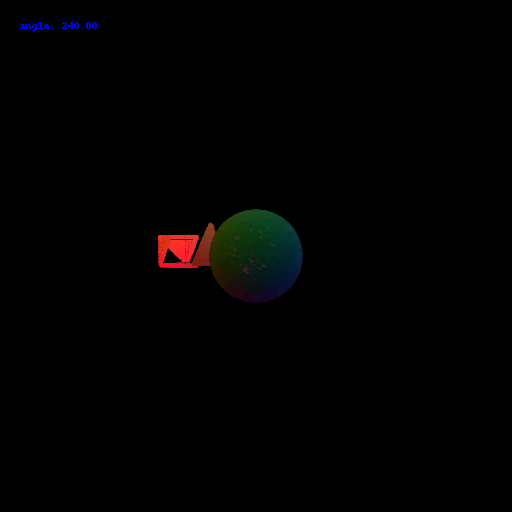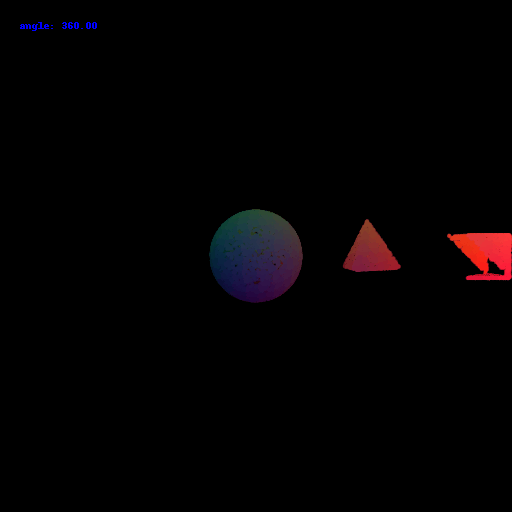Goals: In this assignment, you will learn the basics of rendering with PyTorch3D, explore 3D representations, and practice constructing simple geometry.
You may find it also helpful to follow the Pytorch3D tutorials.

On your webpage, you should include a gif that shows the cow mesh from many continously changing viewpoints.

On your webpage, include a gif with your dolly zoom effect.

On your webpage, show a 360-degree gif animation of your tetrahedron. Also, list how many vertices and (triangle) faces your mesh should have.

There should be 4 vertices and 4 (triangle) faces.
vertices = torch.tensor([[math.sqrt(3),-1.5,-1],[0,-1.2,2],[-math.sqrt(3),-1,-1],[0,2.5,0]])
faces = torch.tensor([[1,0,3],[3,2,1],[0,2,3],[0,1,2]])
On your webpage, show a 360-degree gif animation of your cube. Also, list how many vertices and (triangle) faces your mesh should have.

There should be 8 vertices and 12 (triangle) faces.
vertices = torch.tensor([[1,-1,1],[1,-1,-1],[-1,-1,-1],[-1,-1,1], [1,1,1],[1,1,-1],[-1,1,-1],[-1,1.,1.]])
faces = torch.tensor([[1,0,2],[0,3,2],[2,3,6],[7,6,3],[1,4,0],[1,5,4],[1,2,6],[1,6,5],[0,4,7],[0,7,3],[4,5,7],[4,6,7],])
In your submission, describe your choice of color1 and color2, and include a gif of the
rendered mesh.

Choice of color1 and color2:
color1 = torch.tensor([0,0,1]) # blue
color2 = torch.tensor([1,0,0]) # red
In your report, describe in words what R_relative and T_relative should be doing and include the rendering produced by your choice of R_relative and T_relative.
R_relative is the rotation matrix of the initial camera coordinate system with respect to the new camera coordinate system.
T_relative is the translation of the initial camera coordinate system's origin with respect to the new camera coordinate system's origin.
R_relative=[[0, -1, 0], [1, 0, 0], [0, 0, 1]]
T_relative=[0, 0, 0]
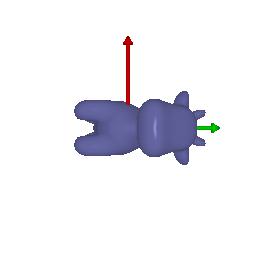
R_relative=[[1, 0, 0], [0, 1, 0], [0, 0, 1]]
T_relative =[0,0,1.5]
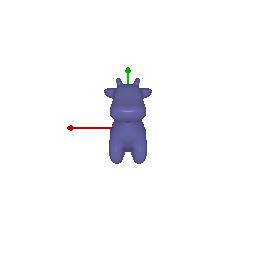
R_relative=[[1, 0, 0], [0, 1, 0], [0, 0, 1]]
T_relative=[0.55, -0.4, 0]
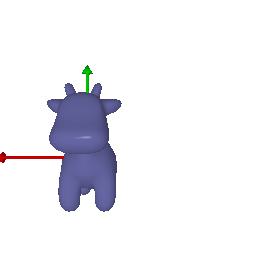
rotate_angle = -90. / 180. * math.pi
R_relative=[math.cos(rotate_angle), 0, math.sin(rotate_angle)], [0, 1, 0], [-math.sin(rotate_angle), 0, math.cos(rotate_angle)]
T_relative=[3., 0, 3]
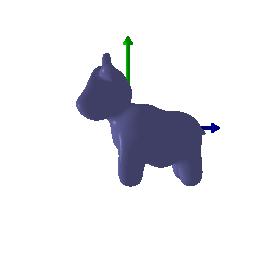
In your submission, include a gif of each of these point clouds side-by-side.
The point cloud corresponding to the first image:

The point cloud corresponding to the second image:

The point cloud formed by the union of the first 2 point clouds:
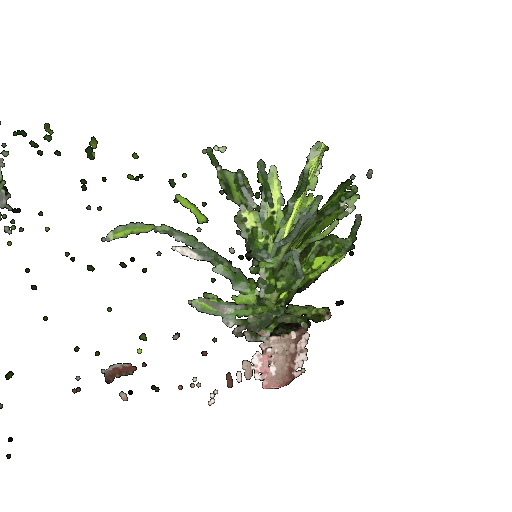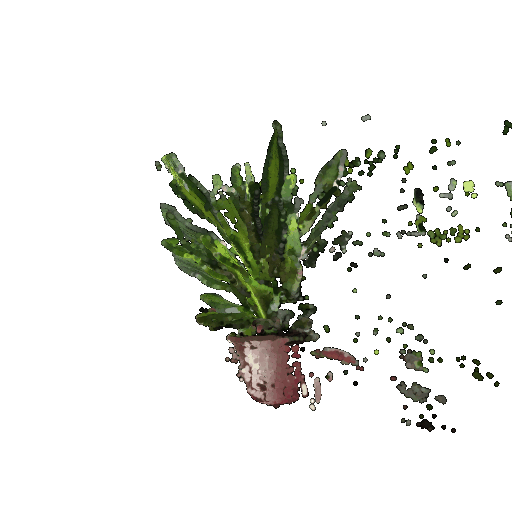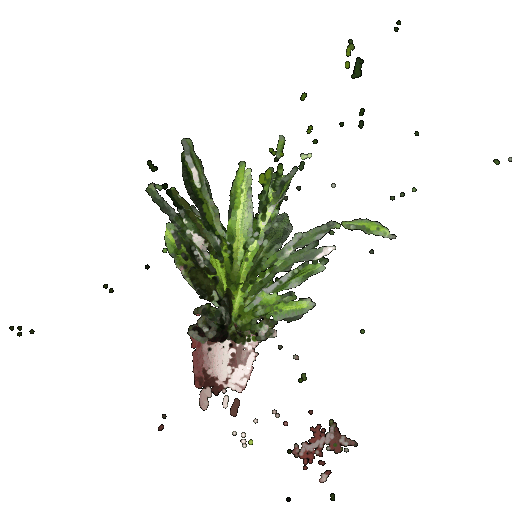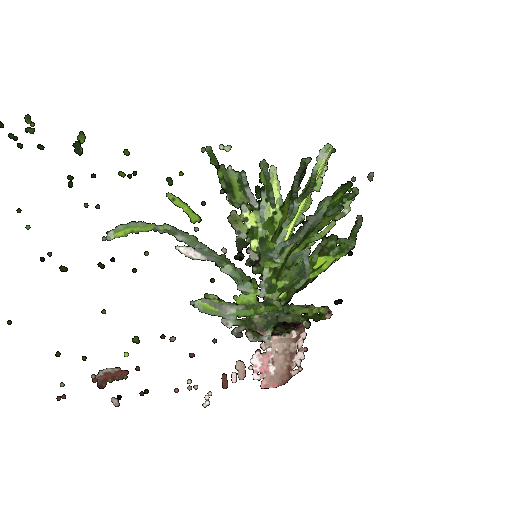
In your writeup, include a 360-degree gif of your torus point cloud, and make sure the hole is visible. You may choose to texture your point cloud however you wish.
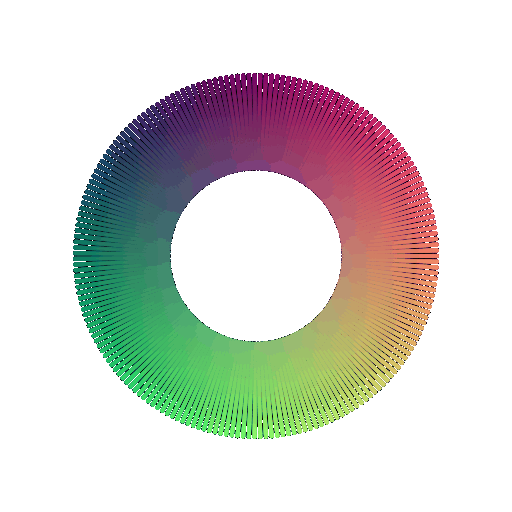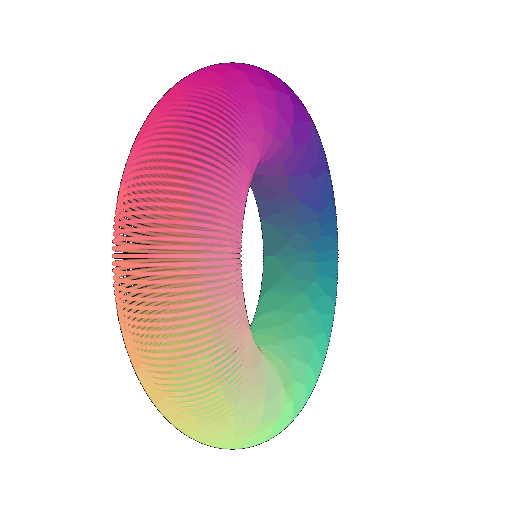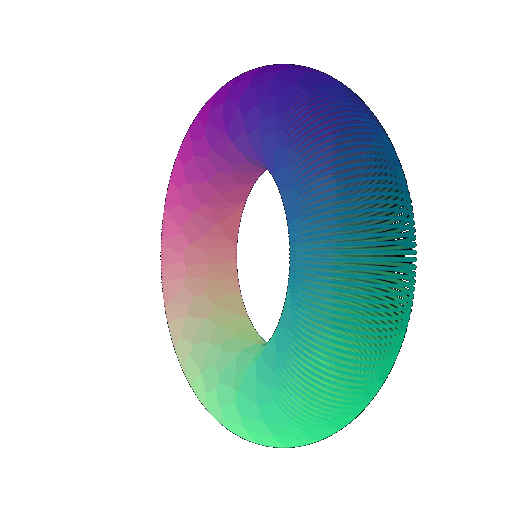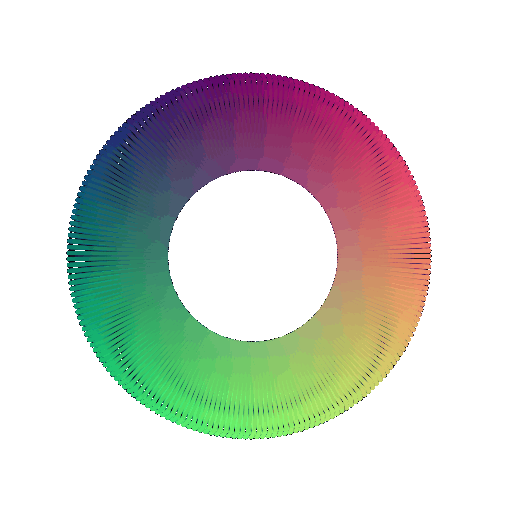
In your writeup, include a 360-degree gif of your torus mesh, and make sure the hole is visible. In addition, discuss some of the tradeoffs between rendering as a mesh vs a point cloud. Things to consider might include rendering speed, rendering quality, ease of use, memory usage, etc.

Point cloud is generated by sampling from the parametric functions. This is easy to use. The sampling stage takes O(n) memory to store the points. During generating points the memory usage depends on the number of parameters in the parametric functions (in torus example we have 2, so O(n^2)). The rendering quality depends on the density of the points. Unlike meshes that we can map textures and shadings on, it will be sparse all the time.
When rendering implicit surfaces (for example, signed-distance function), we have to first create a voxel grid which takes O(n^3) space. Then use matching cube technique to find out the wanted vertices on the surface and create a mesh. The process would take longer. The visualization is better because of the mesh presentation but the location of vertices are not exactly the position where implicit function is a zero-level set. The finer we voxelize, the better results we get.
Include a creative use of the tools in this assignment on your webpage!
An areoplane rendered by mesh and given a new colored texture:

You need to provide the following results to get score
Original cow mesh:

cow pointclouds:
10 points:
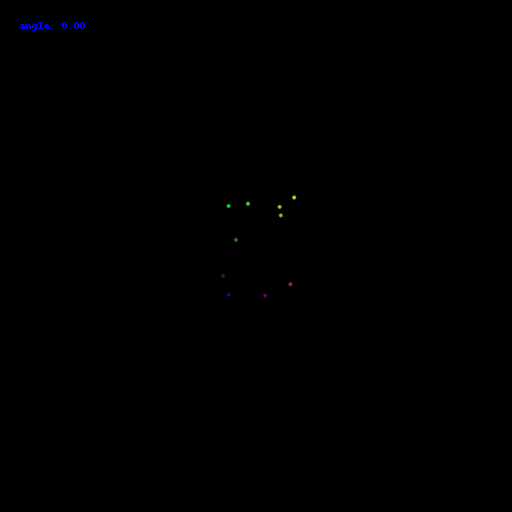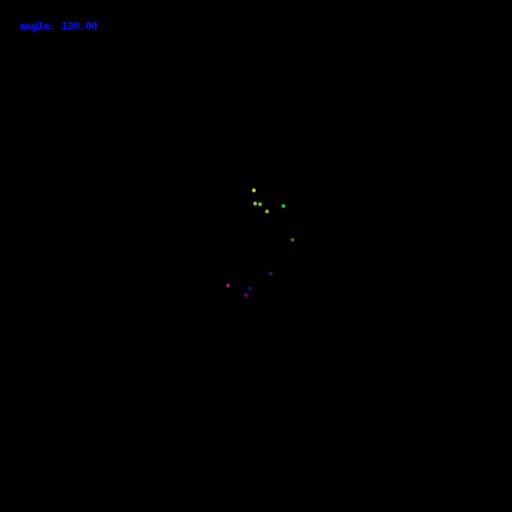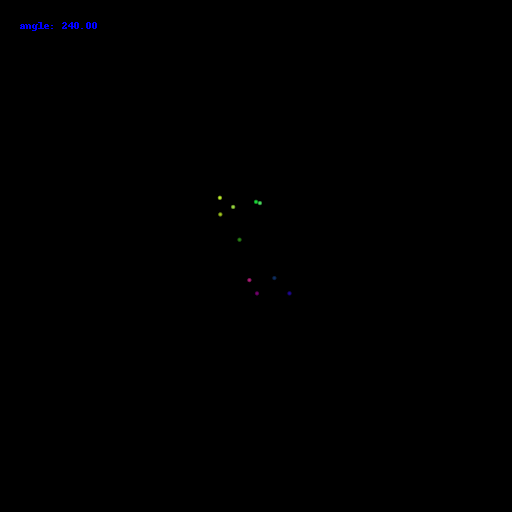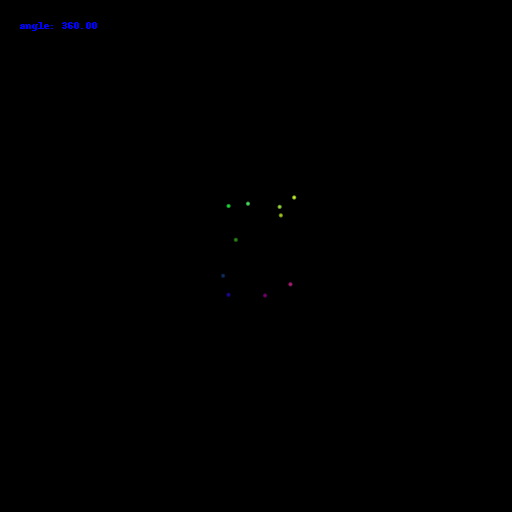
100 points:

1000 points:

10000 points:

Original joint_mesh:
joint_mesh pointclouds:
10 points:

100 points:
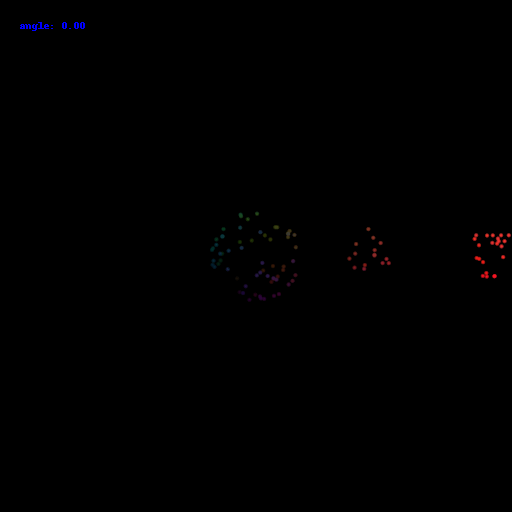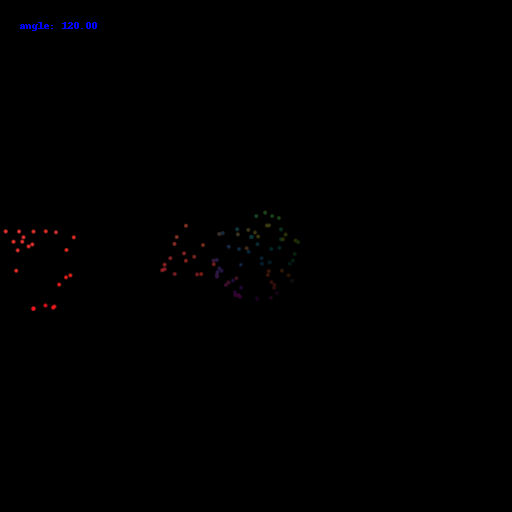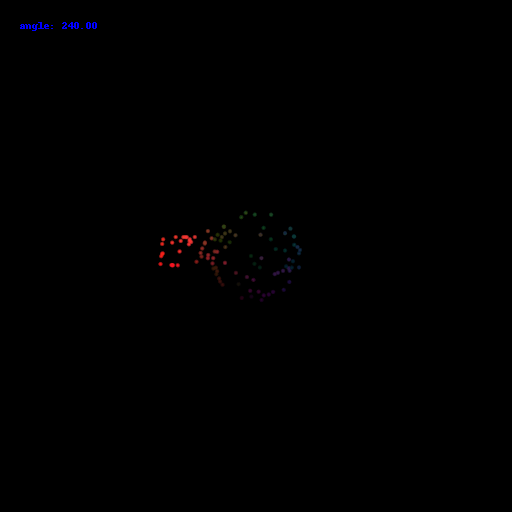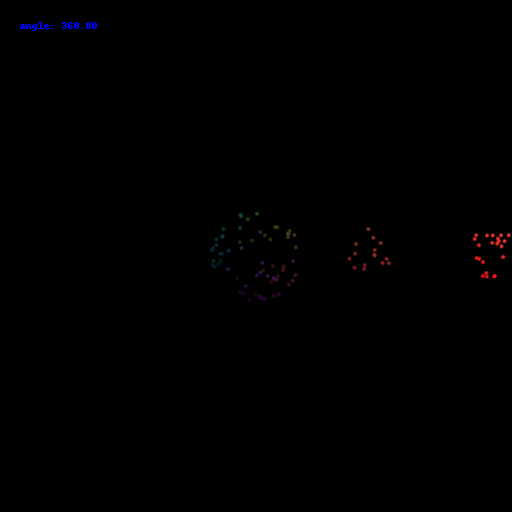
1000 points:

10000 points: